
Fig 1

Fig 2
| Mode Opératoire |
Le banc d'optique
 Fig 1 |
 Fig 2 |
Il est des plus basique.
Des chutes de bois et de contre-plaqué assemblés et collés à l'équerre pour construire le support de la source de lumière à gauche (écran-source)
et l'écran à droite (écran-image).
La source de lumière est contituée par une lampe de type Maglite maintenue dans un trou rond percé dans le support.
Une feuille de bristol blanc est collée sur la face avant et percée au cutter de la lettre F, celle-ci constitue l'objet.
L'écran-image est fait sur le même principe avec une feuille de bristol blanc pour matérialiser l'image de l'objet au travers du réducteur.
Au milieu un tasseau taillé en V comme support de réducteur. Ce dernier est maintenu par un élastique.
Pour l'autocollimation un petit miroir plan aluminé de récupération est utilisé.
Un règle plate graduée de 1 m est utilisée comme guide et également pour faire les mesures. Cette règle peut être remplacée par un tasseau et un mètre à ruban.
Et des serre-joints pour maintenir les différents éléments.
En théorie
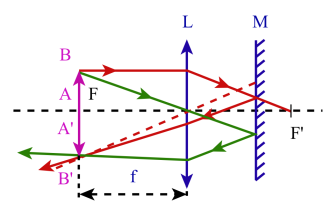
Fig 3
L'ensemble miroir M + lentille mince L est déplacé de manière à former l'image A'B' de l'objet AB dans le plan de l'objet.
La distance entre l'objet et la lentille correspond alors à la distance focale de la lentille.
Voir les liens suivants pour plus de détails
http://uel.unisciel.fr/physique/optigeo/optigeo_ch09/co/apprendre_ch09_01.html
http://uel.unisciel.fr/physique/optigeo/optigeo_ch09/co/apprendre_ch09_06.html
Avec une animation
http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/optiqueGeo/focometrie/autocollimation.php
En pratique
L'écran-image n'est pas utilisé
Il suffit de faire glisser le support du réducteur le long de la règle jusqu'à obtenir une image nette de l'objet F sur l'écran-source.
L'image obtenue sera de même taille mais inversée.
La distance séparant l'écran-source du réducteur correspond alors à la distance focale.
La distance réellement mesurée est en fait celle entre l'écran-source et un point P origine des mesures défini sur le flanc du filetage mâle (voir Fig 4 et Fig 5).
Soit DN cette distance en utilisant le réducteur dans le sens normal de propagation de la lumière (filetage mâle vers la droite).
Soit DI cette même distance mais en orientant le réducteur en sens inverse (filetage mâle vers la gauche), la valeur de cette mesure est différente de celle de DN.
Dans l'approximation des lentilles minces il est possible d'estimer la focale f et la position du centre optique O à partir des valeurs de DN et DI
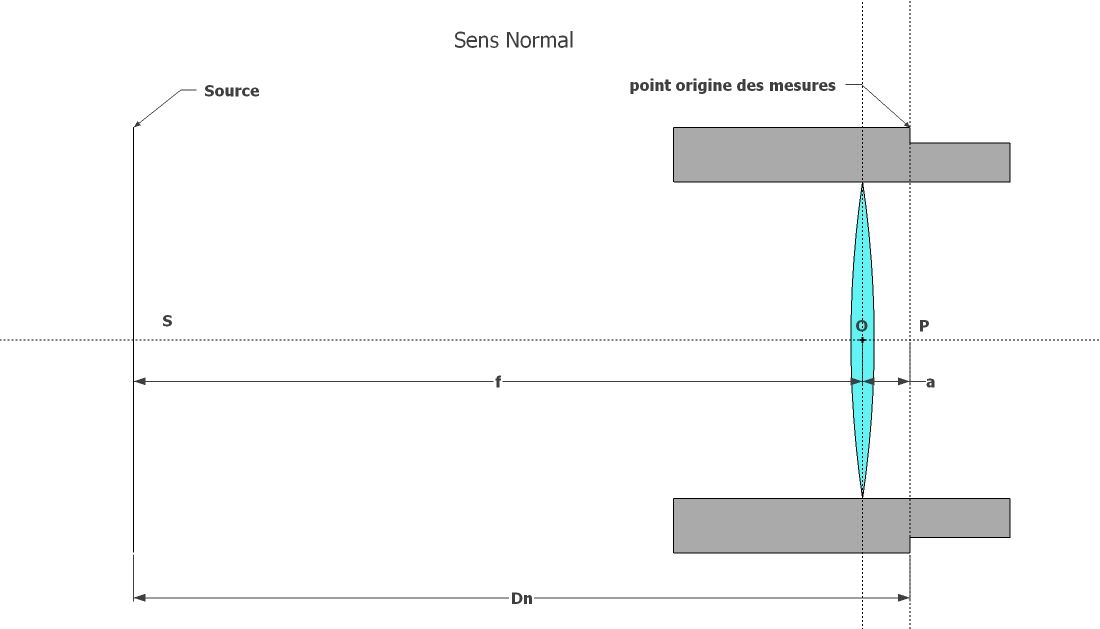 Fig 4 |
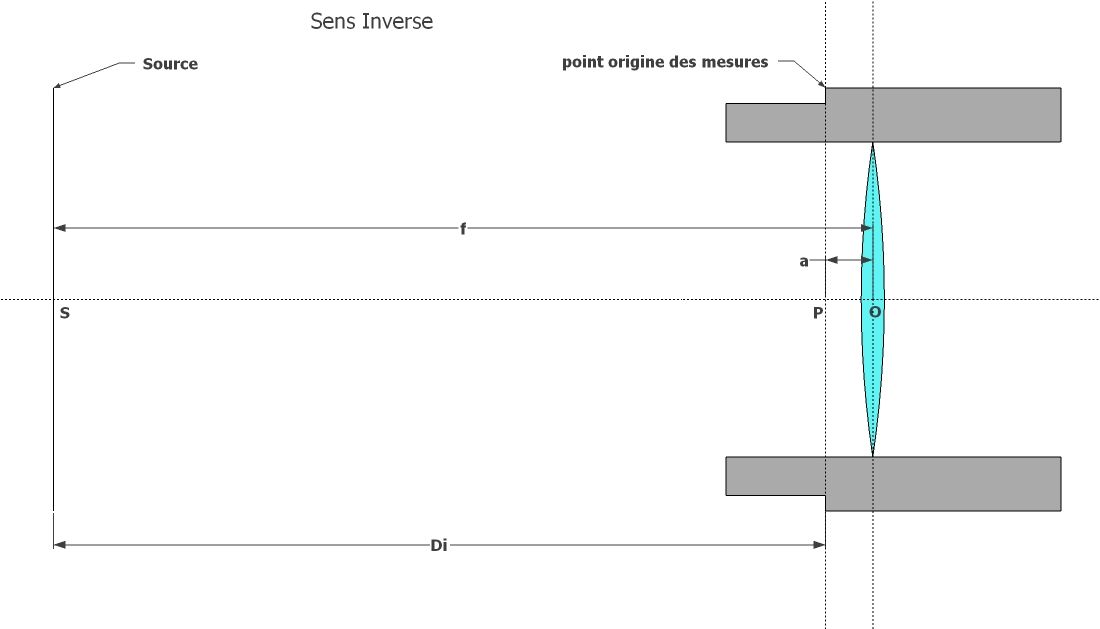 Fig 5 |
Soit a la distance entre les points O et P, et f la focale.
Le réducteur est dans le sens normal d'utilisation (Fig 4)
DN = f + a (eq 1)
En orientant le réducteur en sens inverse (Fig 5)
DI = f - a (eq 2)
En sommant (eq 2) + (eq 1) on obtient la valeur de f
f = (DN + DI) / 2
En faisant la différence (eq 2) - (eq 1) on obtient la valeur de a
a = (DN - DI) / 2
Dans le cas de la Fig 4 la valeur de a est positive.
Elle peut cependant être négative, cela signifie que le centre optique O est à droite du point P et non à gauche comme dessiné dans la Fig 4.
La valeur de a permet de calculer la valeur de Tm, tirage mécanique
Tm = T - a
Pour rappel T = f (1 - R) (formule B de la page d'accueil)
Tm correspond à un backfocus pratique facile à calculer et à mesurer depuis le point P
(flanc du filetage mâle du réducteur) jusqu'au plan du capteur.
Dans le calcul de la longueur des bagues nécessaires, il convient de tenir compte du backfocus de la caméra et des accessoires éventuels (roue à filtres, guideur hors axe, ...)
En théorie
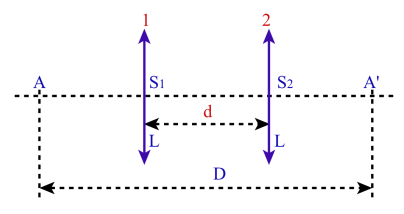
Fig 6
Etant donné une lentille convergente de distance focale f ' et à condition que D > 4 f' il existe deux positions
pour lesquelles la lentille convergente
donne en A' l'image nette d'un objet placé en A.
D = distance entre la source-objet en A et l'écran en A'
d = distance entre les deux points de mesure S1 et S2
f’ = (D² - d²) / 4D
f' = distance focale image
Cette méthode à l'avantage de ne pas faire référence au centre optique pour obtenir la valeur de la focale.
Voir les liens suivants pour plus de détails
http://uel.unisciel.fr/physique/optigeo/optigeo_ch09/co/apprendre_ch09_01.html
http://uel.unisciel.fr/physique/optigeo/optigeo_ch09/co/apprendre_ch09_08.html
Avec une animation
http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/optiqueGeo/focometrie/bessel.php
En pratique
Cette méthode ne nécessite pas de matériel spécialisé, en particulier le miroir plan n'est pas utilisé, elle est donc facile à mettre en oeuvre.
Il suffit de faire glisser le support du réducteur depuis l'écran-source vers l'écran-image le long de la règle jusqu'à obtenir une première image nette
de l'objet F sur l'écran-image à la position S1.
En continuant de faire glisser le support du réducteur, une deuxième image nette plus petite est obtenue en position S2.
Il y a une condition à respecter pour la distance D entre les deux écrans et l'obtention des deux images : D > 4f'
Méthode de Silbermann
En théorie
Cette méthode est un cas particulier de la méthode de Bessel.
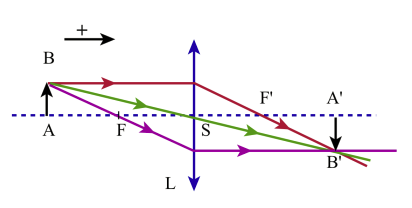
Fig 7
Voir les liens suivants pour plus de détails
http://uel.unisciel.fr/physique/optigeo/optigeo_ch09/co/apprendre_ch09_08.html
Avec une animation
http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/optiqueGeo/focometrie/silbermann.php
En pratique
On diminue la distance D qui sépare l'objet de son image jusqu'à ce que l'image soit identique à l'objet mais renversée.
En divisant la distance correspondante par 4 pour on obtient la distance focale f '.
La mesure de taille de l'image est trop approximative avec les moyens utilisés aussi cette méthode a été abandonnée.
Notions d'optique géométrique
En général
http://uel.unisciel.fr/physique/optigeo/optigeo/co/optigeo.html
Avec une animation
http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/optiqueGeo/
Dernière modification le 17/01/2018
Mis en ligne le 16/01/2018